Notes from Book: Conceptual Mathematics A First Introduction to Categories - William Lawvere
My reading notes from the book
Table of Contents
Preface
goal:
not adding new items to collection
but how keep collection in order
how to find appropriate tool when needed
general concepts that cut across
artificial boundaries dividing
arithmetic, logic, geometry etc.
little about: how to do specialized discussions
but on how to decide what to do in what order
ch01: Galileo and multiplication of objects
1. Introduction
basic notion: category
which underlies all the others
a mathematical universe
2. Galileo and the flight of a bird
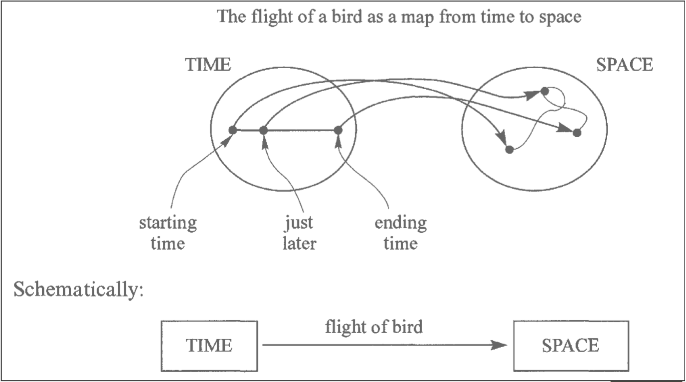
motion:
a map from time to space
/Users/mertnuhoglu/Dropbox/public/img/ss-49.png
why did galileo focus on vertical motion:
space = plane x line
two maps
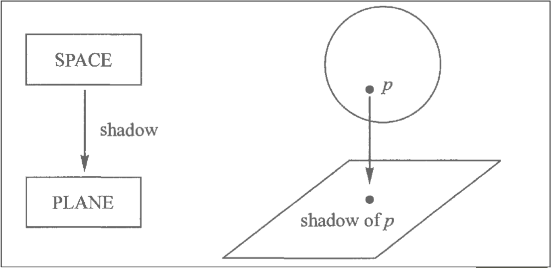
shadow map:
/Users/mertnuhoglu/Dropbox/public/img/ss-50.png
sun is direvtly overhead
for each point in space
you get a shadow point on plane
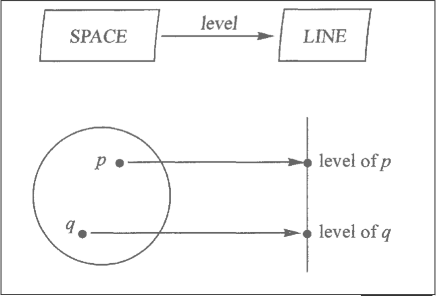
level map:
/Users/mertnuhoglu/Dropbox/public/img/ss-51.png
a pole stuck into ground
for each point in space there is a corresponding point on the line (at the same level)
together we have:
[space] level -> [line]
[space] shadow -> [plane]
they reduce each problem about space to 2 simpler problems
one for plane
one for line
suppose you keep all positions over time too
you have
[time] flight of a bird -> [space]
we can then get:
[time] flight of a bird -> [space]
[space] level -> [line]
[space] shadow -> [plane]
we can get these two maps:
[time] level of flight of bird -> [line]
[time] shadow of flight of bird -> [plane]
now space disappeared from the picture
galileo's discovery:
from two simpler motions
recapture motion in space
if simpler motions are continous
motion in space is continous too
equation
[space] level -> [line]
[space] shadow -> [plane]
is equivalent to:
space = plane x line
3. Other examples of multiplication of objects
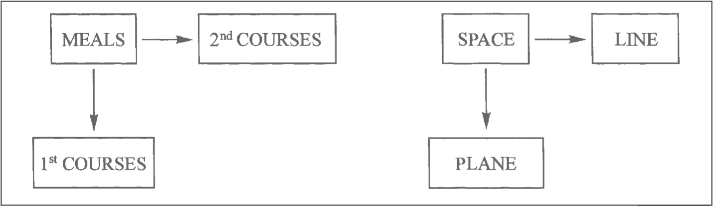
restaurant has two lists
/Users/mertnuhoglu/Dropbox/public/img/ss-52.png
option for first course
option for second course
a meal involves one item from each list
diagram
[meals] -> [1st course]
[meals] -> [2nd course]
similar to Galileo's diagram:
[space] level -> [line]
[space] shadow -> [plane]
cylinder = ellipse x line_segment
ex: from logic
"A and B"
John is sick and Mary is sick
we can deduce A and B:
[John is sick and Mary is sick] -> [John is sick "A"]
[John is sick and Mary is sick] -> [Mary is sick "B"]
suppose: we can deduce A,B from C
[C] -> [A]
[C] -> [B]
then
[C] -> [A and B]
Part I: The Category of sets
Article 1: Sets, maps, composition
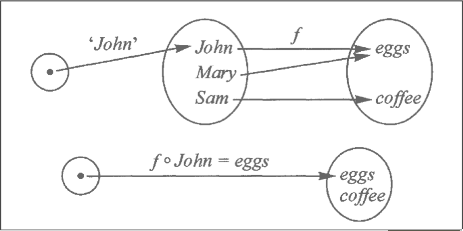
first become familiar: category of finite sets and maps
object: a finite set
map f:
consists of
a set A: domain
a set B: codomain
a rule assigning each element a to b
f(a)
f of a
f ○ a
other names
function, transformation, operator, arrow, morphism
endomap:
domain and codomain are same object
simple endomap: 1_A
identity map
f(a) = a
external diagram:
[A] f -> [B]
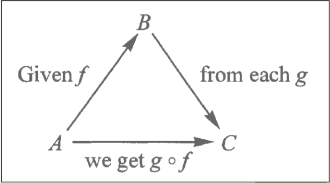
composition of maps
gives all the dynamics to the notion of category
[A] g -> [A] f -> [B]
f ○ g
f following g
f of g
definition: category (mathematical universe)
data:
objects: A,B,C...
maps: f: A -> B
identity maps: (one per object): 1_A: A -> A
composition of types:
assigns to each pair of maps of type:
[A] g -> [A] f -> [B]
another map called "f following g"
[A] f·g -> [C]
rules:
identity laws:
a) if [A] 1_A -> [A] g -> [B]
then [A] g·1_A = g -> [B]
b) if [A] f -> [B] 1_B -> [B]
then [A] 1_B·g = g -> [B]
associative law
if [A] f -> [B] g -> [C] h -> [D]
then [A] h·(g·f) = (h·g)·f -> [D]
singleton set: a set with one element
call this set: 1
definition: A point of a set X is a map 1 -> X
if A is familiar set,
/Users/mertnuhoglu/Dropbox/public/img/ss-53.png
a map from A to X is called: A-element of X
thus 1-elements are points
ch02: Sets, maps and composition
1. Review of Article 1
3. external diagram
external diagram
shows domains
internal diagram
shows instance by instance mapping
4. Problems on the number
#: number of possible maps
A -> B
if B has 1 elements
#: 1
if A has 1 elements
#: n_B
if A has zero elements
#: 1
if B has zero elements
#: 0
if A and B are empty
#: 1
ch03: Composing maps and counting maps
Part II: The algebra of composition
Article II: Isomorphisms

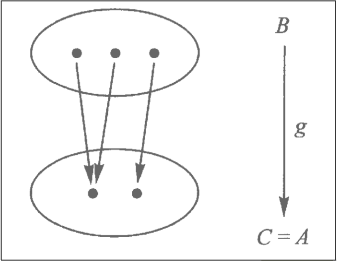
1. Isomorphisms
similarities between collections
ex: same number of elements
what special properties does map f have then?
one-to-one: injective and surjective
then there is an inverse map g for f
g·f = 1_A
f·g = 1_B
definition:
a map [A] f -> B is called an isomorphism (or invertible map)
if there is a map [B] g -> A
for which g·f = 1_A and f·g = 1_B
g is inverse for f
objects A, B are isomorphic if there is at least one isomorphism
isomorphic ≅ same-size
has certain properties
reflexive: A is isomorphic to A
symmetric: if A is isomorphic to B, then B is isomorphic to A
transitive: if A -> B and B -> C, then A -> C isomorphic
these properties come from associative and identity laws
ex: cartesian geometry
analytic approach to geometry starts with an isomorphism:
[P] f -> [ℝ²]
assigns each poit a coordinate-pair
this translated difficult problems in geometry into easier problems in algebra (or opposite way)
ex: a map f cannot have two different inverses
2. General division problems: Determination and choice
/Users/mertnuhoglu/Dropbox/public/img/ss-68.png
two sorts of division problems for maps:
determination (extension) problem
given f and h, what are all g for which h = g·f
choice (lifting) problem
g and h given. what are f for which h = g·f
determination problem
we say:
h is determined by f
h depends only on f
a particular solution g: determination of h by f
h is a function of f
why is this division problem called determination problem
ex1: B is a one-element set
then:
h(x) = (g·f)(x) = g(f(x)) = g(b)
for all x in A
h is called: constant
because even x varies, h(x) is same
ex2: a choice problem
/Users/mertnuhoglu/Dropbox/public/img/ss-69.png
B has three elements
A = C has two elements
g·f = 1_A
so f is inverse of g
for a given g, there are two f that satisfy g · f = 1_A
for f(x) = z, z ∈ B
for each x, we need to choose one z value
but since n_A < n_B we have multiple choices of z for some x
we can choose any option for those x
@mine:
inverse fonksiyon tek bir tane olur demiştik, nasıl oluyor da çok sayıda olabildi?
choice problem'deki f g'nin inverse'i değil, sadece tek bir taraftan inverse:
g·f = 1_A
f·g ≠ 1_B
ex3: Galileo's determination problem
Time -> Distance
Weight !-> Distance
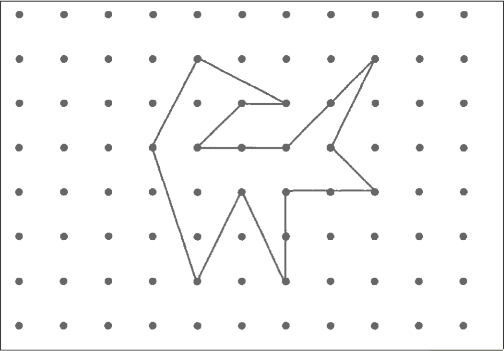
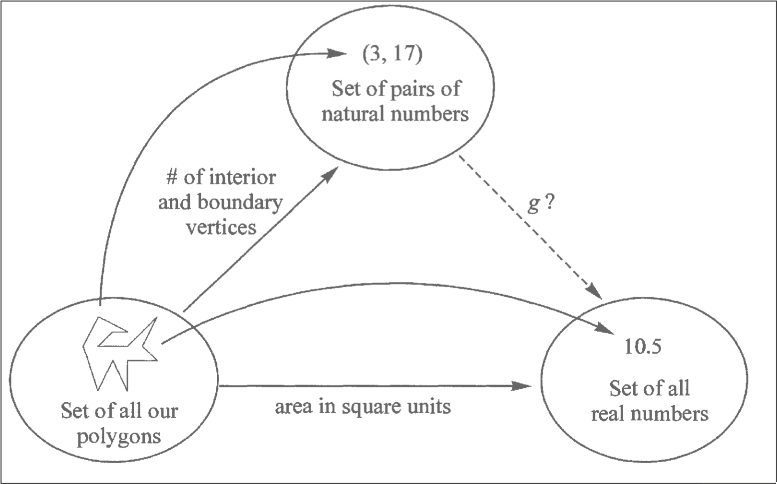
ex4: Pick's formula
/Users/mertnuhoglu/Dropbox/public/img/ss-70.png
points in plane
polygonal figure
area is a function of
dots inside
dost at boundary
/Users/mertnuhoglu/Dropbox/public/img/ss-71.png
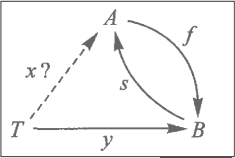
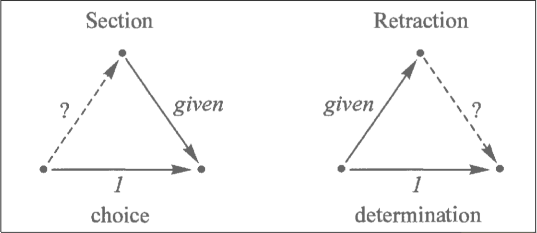
3. Retractions, sections, and idempotents
retraction (section) problem:
determination/choice problem where h is an identity map
definition:
if [A] f -> [B]
a retraction for f is a map [B] r -> A
for which r·f = 1_A
a section for f is a map [B] s -> A
for which f·s = 1_B
retraction problem is a determination problem
section problem is a choice problem
similarity to multiplication
multiplication annd reciprocals problem
some have
1 answer
0 answers
infinite answers
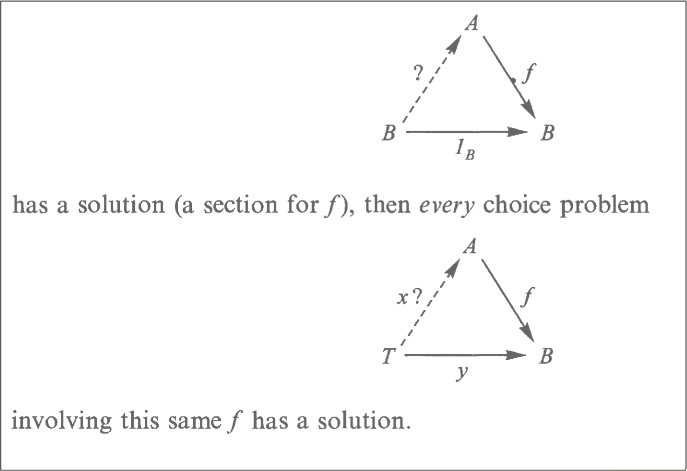
proposition 1:
/Users/mertnuhoglu/Dropbox/public/img/ss-72.png
if single choice problem has a solution (section for g), then every choice problem involving same g has a solution
/Users/mertnuhoglu/Dropbox/public/img/ss-74.png
formally:
if [A] f -> [B] has a section
then for any T and map: [T] y -> [B]
there exists a map [T] x -> A
for which f · x = y
mine:
eğer f sağ tersinirse, her y için x vardır öyle ki: f·x = y
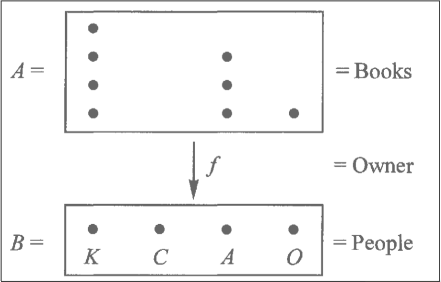
ex: representatives
170210.06.01.jpg
s for f is thought as a choice of representatives
A: citizen
B: city
f: city where citizen resides
f:
| Ahmet | NY |
| Ali | NY |
| Ayşe | LA |
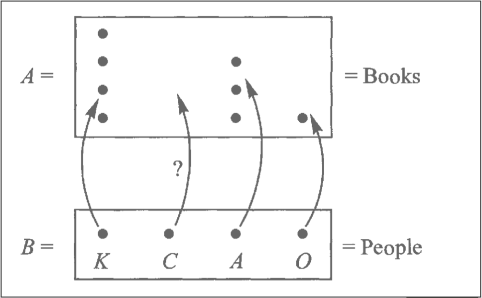
what is s?
one choice for s:
| NY | Ahmet |
| LA | Ayşe |
[A] n-1 [B]
going from B to A: take one representative from A
dual of proposition 1: 1*
if r has a solution for single determination problem
then every determination problem with the same f has a solution
mine: mnemonics for retraction/section:
for any g there exists t:
if f has retraction
t·f = g
if f has section
f·t = g
mine: why is there dual but not triple?
iki operasyon arasındaki ilişkinin sıralaması ancak iki türlü olabilir:
önce/sonra
üçüncü bir seçenek yok.
proposition 2:
if f has retraction r·f=1_A
for any pair of maps:
[T] x1 -> [A]
[T] x2 -> [A]
if
f·x1 = f·x2
then
x1 = x2
definition: f satisfies proposition 2
f is injective for maps from T
definition: f is injective for maps from T for every T
f is injective or is a monomorphism
mine: mnemonics for 1-n between A-B
170210.08.01
ilk kime f uygulanıyorsa, o kümeden 1-n olmalı
r·f = 1_A
[A] 1-n [B]
f·s = 1_B
[A] n-1 [B]
s: sağ. ilk s uygulanır. geri dönme fonksiyonu B'den gider. B:1 A:n
neden ilk kime f uygulanıyorsa, o küme 1 oluyor?
daha az elemanı olmalı ki, o kümeye geri dönebilelim
daha fazla elemanı olan kümenin bazı elemanları aynı karşı elemana bağlanmak zorunda.
mine: mnemonics for injective/surjective
injective when r·f=1_A
A:1 B:n
x: T -> A bağıntıları injective
injective: B'nin alt kümesi
A'dan birebir
proposition 2*: dual of 2
f: A -> B has section: f·s = 1_B
for any T and t1,t2:
t1: B->T
t2: B->T
if t1·f = t2·f
then t1 = t2
definition: a map f with this cancellation property (if t1·f = t2·f then t1 = t2) for every T is called an epimorphism
comparison
monomorphism: f·t1 = f·t2 => t1 = t2 (cancellation from left)
epimorphism: t1·f = t2·f => t1 = t2 (cancellation from right)
proposition 3: transivity
if f: A -> B has a retraction and g: B -> C has a retraction
then g·f: A -> C has a retraction
definition:
an endomap e is called idempotent if e·e = e
theorem: uniqueness of inverses
if f has both a retraction r and a section s then r = s
4. Isomorphisms and automorphisms
definition: isomorphism (again)
f is an isomorphism
if there is f' which is both a retraction and section for f
f': inverse map for f
relation between A and B when isomorphism exists
A B have same number of elements
but we don't count elements
if A and B are isomorphic, then there exists an isomorphism between A and B in the category
definition: automorphism
f is both an endomap and isomorphism
how many isomorphisms are there between A and B
same number as automorphisms
Aut(A): set of automorphisms
Isom(A,B): set of isomorphisms
Aut(A) is non-empty because at least 1_A is an example
automorphism in sets: called permutation
Session 4: Division of maps: Isomorphisms
1. Division of maps versus division of numbers
| Numbers | Maps |
| multiplication | composition |
| division | ? |
division: reverse operation
some solutions are not unique
no solution
many solutions
typical for composition of maps
easiest case: division of maps produces exactly one solution
2. Inverses versus reciprocals
definition:
if f:A->B has an inverse g:B->A satisfying both:
g·f=1_A and f·g=1_B
f is an isomorphism and invertible map
uniqueness of inverses:
any map f has at most one inverse
3. Isomorphisms as divisors
4. A small zoo of isomorphisms in other categories
algebra groups:
R,+
R,*
ex:
R,*
f x = 2x
h x = 1/2 x
both respect composition
h is inverse for f
so f is isomorphism
ex: geometry
/Users/mertnuhoglu/Dropbox/public/img/ss-75.png
object: polygonal figure
map: any map which preserves distances
Session 5: Division of maps: Sections and retractions
1. Determination problems
f determines another quantity h
ex:
cylinder with gas inside
heat the system
volume of gas increases
raises the piston
cool the system to original temperature
gas returns to original volume
we suspect: temperature determines the volume
diagram
[States of system] h -> [Volumes]
[States of system] f -> [Temperatures]
[Temperatures] g -> [Volumes]
if there is a g for which:
h = g·f
g is called a determination of h from f
generalize this
/Users/mertnuhoglu/Dropbox/public/img/ss-76.png
suppose we have: f: A -> B and C
then every map from B to C
can be composed with f
to get a map A -> C
thus f gives us a process
that takes maps B -> C
andn gives maps A -> C
determination problem:
Given maps f: A -> B and h: A -> C
find all maps from B to C st g·f = h
this problem asks
is h determined by f?
ex:
A: students
B: gender
C: yes/no
f: A -> B gives gender of student
h: A -> C did student wear hat today?
case1: h = g·f
g: B -> C
whether a student is female/male can tell whether he wears hat or not
then h is determined by f
ex 1: to find a proof g that h is determined by f
a: points
2. A special case: Constant maps
suppose: B is one-element
then f is known
then h must send all elements of A to same element of C
such a map is called a constant map
definition:
a map that can be factored through 1 is called a constant map
3. Choice problems
looking for f instead of g
choice problem because we need to choose for each a ∈ A an element b ∈ B st.
g(b) = h(a)
ex:
C: towns
A: people
h: resides in town
B: supermarkets
g: location of supermarket
f: supermarket to shop
f: each person must choose a supermarket in his town
ex 2: existence of choice maps
a: if there is an f with g·f = h
then h and g satisfy:
∀ a ∈ A: ∃ b ∈ B st
h(a) = g(b)
4. Two special cases of division: Sections and retractions
special case of choice problem:
A = C
h: identity map 1_A
definition:
f: A -> B is a section of
g: B -> A if g·f = 1_A
application of a section:
solution to choice problem for any map h: A -> C
how?
variant of
if you have 1/2 don't divide by 2; multiply by 1/2 instead
suppose we have a choice problem
question: order matters
/Users/mertnuhoglu/Dropbox/public/img/ss-77.png
mine: mnemonics
determination problem: what hat to wear today?
determined by gender of student
choice problem: each person choose a market
section/retraction
g·f = 1
f: section
f is searched in choice problem
g: retraction
g is searched in determination problem
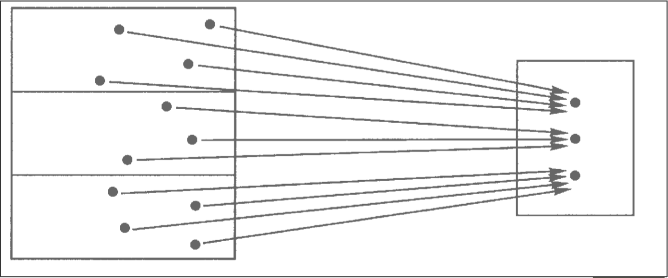
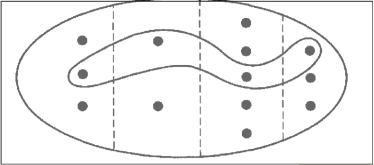
5. Stacking or sorting
ex:
A: books in classroom
B: people in same classroom
"belongs to": A -> B
person that brought the book into classroom
visualize it by stacking/sorting:
/Users/mertnuhoglu/Dropbox/public/img/ss-78.png
stacks picture helps us to find all sections of map
/Users/mertnuhoglu/Dropbox/public/img/ss-79.png
Chad didn't bring a book
thus: no section for f
in order f to have a section
every element of B must have non-empty stack
ie. ∀ b ∈ B, there must ∃ a ∈ A st f(a) = b
number of sections
numbers of each stack multiplied
6. Stacking in a Chinese restaurant
Session 6: Two general aspects or uses of maps
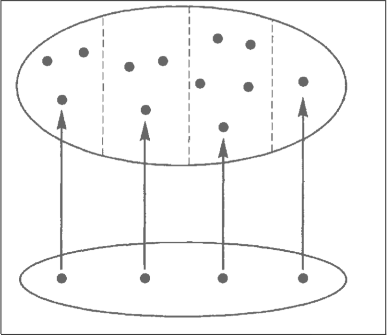
1. Sorting of the domain by a property
stacking gibi sorting kelimesi de kullanılabilir
g: X -> B
we say: g gives rise to a sorting of X into B sorts
names:
sort: elements in B
/Users/mertnuhoglu/Dropbox/public/img/ss-80.png
we say: the map is a B-valued property on X
g is a stacking of the elements of X into B stacks
in no sort is empty, then the map has a section
partitioning: such maps
say: a map X -> B produces a structure in the domain X
map: B-valued property
ex: people: X, B: hair color
map: from the set of people to set of colors
people are sorted by property of hair color
2. Naming or sampling of the codamin
f: A -> X
we say: f is a familiy of A elements of X
we say: map from A to X is an A-shaped figure in X
we say: A-element is the same as figure of shape A
ex: each students point out a country on a globe
then we say: Ali's country, Danny's country
we say: exemplifying, parameterizing maps:
f:A->X is to parameterize part of X by moving along A following f
3. Philosophical explanation of the two aspects
Reality consists of things in their motion and development
other things reflect it, such as words, books,
small objects:
1-n ilişkideki 1 tarafı
small domain sets (listing)
small codmain sets (properties)
Session 7: Isomorphisms and coordinates
1. One use of isomorphisms: Coordinate systems
ex:
plot: A -> X
coordinate: X -> A
coordinate · plot = 1_A
plot · coordinate = 1_X
cartesian system:
first: ℝ2 -> ℝ
second: ℝ2 -> ℝ
ex: first(3.12, 4.7) = 3.12
q is a point in plane
[1] q -> [P] coordinate -> [ℝ2] first -> [ℝ]
@mine: her bir sabit değer (constant value) aslında bir morphismdir 1 kümesinden P kümesine
böylece tüm değerleri de morphism olarak tanımlıyoruz
to get a number:
first·coordinate·q
called: first coordinate of q
once we fixed an isomorphism: f: A -> X
we can tread A and X as the same object
because we have inverse maps to translate
2. Two abuses of isomorphisms
Session 8: Pictures of a map making its features evident
why the word "section"
short for cross section
section'ın imajı ana kümeden daha küçüktür
onun bir kesitidir
name: choice of representatives: another name for section
Section 9: Retracts and idempotents
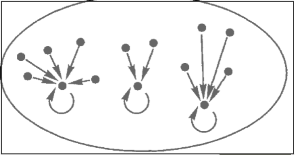
1. Retracts and comparisons
isomorphism: A ≅ B then
there is at least one invertible map from A to B
for finite sets:
A and B have same number of points
maps from a singleton set 1
how to say: A is at most as big as B
definition: A ◁ B means that there is at least one map from a to B
it has two properties:
R, for reflexive
since there is the identity map
T, for transitive
if A ◁ B and B ◁ C then A ◁ C
for sets: comparing objects needs additional method
remember: a section-retration pair: A is at most as big as B
definition: A is a retract of B means:
there are maps [A] s -> [B] r -> [A]
with r·s = 1_A
we write A ≤_R B
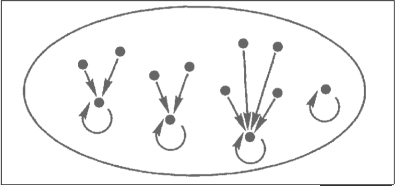
2. Idempotents as records of retracts
idempotent functions
A unary operation (or function) is idempotent if, whenever it is applied twice to any value, it gives the same result as if it were applied once; i.e., ƒ(ƒ(x)) ≡ ƒ(x). For example, the absolute value function, where abs(abs(x)) ≡ abs(x), is idempotent.
e = s·r is idempotent
ex:
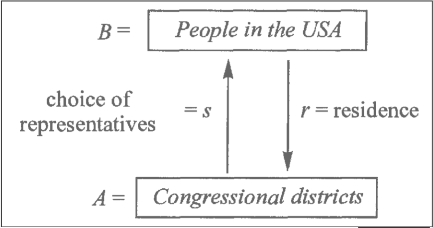
/Users/mertnuhoglu/Dropbox/public/img/ss-81.png
B: people in USA
A: districts
s: choice of represantitves
r: residence
fixed points: image of e = s·r
they are congress represantitives
it is isomorphic to set of districts
e: idempotent map
/Users/mertnuhoglu/Dropbox/public/img/ss-82.png
r is as sorting of B by A
/Users/mertnuhoglu/Dropbox/public/img/ss-83.png
definition:
if e:B->B is an idempotent map
a splitting of e consists of an object A
together with maps:
s: A -> B
r: B -> A
r·s = 1_A
s·r = e
crucial idea:
all essential information about A, r, s
are contained in B and e
4. Three kinds of retract problems
r,s
r: sorting of B into A sorts
s: choosing for each sort an example of that sort
problem: a section s of r
ex: museum director's problem
B: mammals
A: specifies of mammals
r known
s unknown
job: choose a section s of r
ie. selecting one example for each species
opposite (dual) problem
ex: bird watcher's problem
manual gives an example of each species (sampling/exempliying map s)
B: birds observerd
A: species of birds
s known
r unknown
job: assign each bird he sees a species
@mine
bu problem tasnif problemi
A: sınıflar
B: örnekler
class/instance
type/instance meselesi
third problem: idempotent
ex: child sees a variety of animals. young child learns animals
tries to select an idempotent endomap e
B = Animals
e: Animals -> Animals
e: assigns each animal to most familar animal
having selected e, he is asked to split this idempotent into sorts of animals
B: Animals
A: sorts of animals
sr = e
rs = 1_A
s: assigns to each sort of animal, the most familiar example
r: assigns to each animal, its sort
museum director's problem:
choosing a cross-section
/Users/mertnuhoglu/Dropbox/public/img/ss-85.png
bird watcher's problem:
view s as a sampling of B by A
choosing for each bird the most similar bird identified in the manual s
/Users/mertnuhoglu/Dropbox/public/img/ss-86.png
child's problem:
selection of the idempotent
then splitting by idempotent
5. Comparing infinite sets
Composition of opposed maps
test for equality of maps
for f: A -> B, h: B -> A:
f = h
iff f·a = h·a for every point a: 1 -> A
Session 10: Brouwer’s theorems
1. Balls, spheres, fixed points, and retractions
Brouwer fixed point theorem
I: line segment
suppose: f: I -> I is a continous endomap
then this map must have a fixed point
f(x) = x
D is a closed disk. f a continous endomap of D. Then f has a fixed point